Your Ultimate Factorial Calculator: A Fun & Easy Guide to n!

Have you ever wondered how many ways you can arrange your favorite books on a shelf? Or how many different orders you could run a series of errands? What seems like a simple question can lead to a surprisingly large number of possibilities. This is where the magic of factorials comes in!

But what is a factorial, and how do you calculate it, especially for large numbers? Manually multiplying a long string of numbers is tedious and prone to error. That’s exactly why we created our Factorial Calculator. It’s an easy-to-use online tool that does all the heavy lifting for you, delivering instant and accurate results for any number you can think of. Let’s dive into the fascinating world of factorials and see how this tool can make your math life much simpler.

What is a Factorial?

In simple terms, a factorial is just a fancy way of saying “multiply all the whole numbers from this number down to 1.”

It’s represented in math by the exclamation mark (!). So, when you see 5!, you don’t read it as “FIVE!” in an excited voice, but as “five factorial.” It means:

5! = 5 × 4 × 3 × 2 × 1 = 120

See? It’s not as scary as it looks. The factorial function is a fundamental concept in mathematics, especially in areas like:

• Probability: Figuring out the chances of something happening.
• Permutations and Combinations: Counting the number of ways to arrange or select things.
• Algebra and Calculus: Appearing in many important formulas and series.

At its heart, a factorial answers the question: “How many different ways can I arrange a set of distinct items?”

How Does the Factorial Calculator Work?

Our Factorial Calculator is designed to be incredibly straightforward. It automates the process we just described. You provide the number, and the calculator instantly performs the multiplication sequence for you.

Think of it as your personal math robot. You tell it, “Hey, what’s 10!?” and it immediately runs the calculation: 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 and gives you the answer: 3,628,800.

Real-World Example: Let’s say you have 5 different ice cream flavors and you want to know how many possible orders you could serve them in. Instead of writing out all the combinations, you just open our Factorial Calculator, enter 5, and click calculate. In a flash, it tells you the answer is 120 unique ways. It’s that easy!

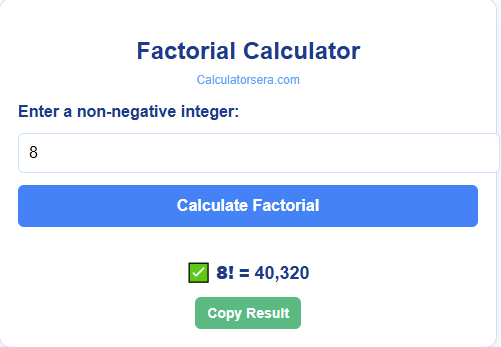
Step-by-Step: How to Use the Factorial Calculator

Using our tool is a breeze. Just follow these simple steps:

1. Navigate: Go to Calculatorsera.com and find the Factorial Calculator.
2. Enter: Type any non-negative whole number into the input field. Let’s try 7.
3. Calculate: Press the “Calculate” button.
4. Result: Instantly see the result: 7! = 5040.

You can try different numbers to explore how rapidly factorials grow. What happens when you enter 10? Or 15? It’s fascinating to see the results appear instantly, even for numbers that would take minutes to calculate by hand.

The Factorial Formula

Every math concept has a formula, and the factorial is beautifully simple. The formula for the factorial of a number *n* is:

n! = n × (n − 1) × (n − 2) × ⋯ × 1

In plain English: Start with your number, and multiply it by every positive integer less than itself, all the way down to 1.

Let’s look at a few examples:

• 4! = 4 × 3 × 2 × 1 = 24
• 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

Special Cases to Remember

There are two special factorials that everyone should know:

• 1! = 1 (This makes sense, as there’s only one way to arrange one item).
• 0! = 1

Wait, why is zero factorial equal to one? This often seems strange at first! Think of it as the mathematical definition for “doing nothing.” There is exactly one way to arrange zero objects—that is to have no arrangement at all. It also makes many mathematical formulas consistent and work properly. So, just remember: 0! = 1.

Example Chart: How Factorials Grow

One of the most amazing things about factorials is how incredibly fast they increase. They start small but quickly explode into enormous values. This bar chart below shows the explosive growth of factorials for the first few numbers. It visually demonstrates why a Factorial Calculator is so essential for larger values!

As you can see, the values start to skyrocket! From just 7! = 5040, it jumps to 8! = 40,320 and 10! = 3,628,800. This is why we call this kind of growth “combinatorial explosion.”

Where Are Factorials Used?

You might think factorials are just abstract math concepts, but they pop up in many real-world scenarios, especially when dealing with arrangements and choices.

• Math & Probability: Calculating the odds of winning a lottery, or the probability of being dealt a specific hand in cards.
• Computer Science: Used in algorithms, especially those involving “recursion” (a function that calls itself), and in analyzing how long certain tasks take to complete.
• Everyday Life: Any situation where you need to count possibilities.
  • Example: If you have 4 different tasks to do, how many different orders could you do them in? The answer is 4! = 24 possible schedules.

Fun Real-Life Examples

Let’s make factorials even more relatable with some fun examples:

• Arranging Books: You have 3 favorite books on your shelf. How many ways can you order them?
  • 3! = 3 × 2 × 1 = 6 different arrangements.
• Seating Friends: You need to seat 5 friends in a row of chairs for a photo. How many possible seating orders are there?
  • 5! = 5 × 4 × 3 × 2 × 1 = 120 different ways to seat them.
• Pizza Toppings: A pizza shop lets you choose the order in which they put on 7 toppings. How many different “layering” experiences could you create?
  • 7! = 5040 unique pizzas, just based on the order of toppings!

Benefits of Using an Online Factorial Calculator

Why should you use our online factorial calculator? The advantages are clear:

• Speed and Accuracy: Get instant, error-free results. No more manual multiplication mistakes.
• Saves Time: Calculating something like 15! by hand would take several minutes. Our calculator does it in less than a second.
• Homework Helper: Perfect for students to check their work and understand factorial concepts better.
• Accessibility: It’s free, available 24/7 on Calculatorsera.com, and works on any device with an internet connection.
• Handles Large Numbers: Effortlessly computes factorials for numbers that are simply impractical to calculate manually.

Tips for Learning Factorials

Getting comfortable with factorials is easy with a few simple tips:

1. Memorize the Small Ones: Know 1! through 5! by heart. It builds a strong foundation.
2. See the Pattern: Notice that each factorial is just the previous one multiplied by the next number. For example, 6! = 5! × 6 = 120 × 6 = 720.
3. Connect to Real Life: Always think of an arrangement (books, people, colors) when you see a factorial. It makes the concept stick.
4. Use the Tool: Don’t be shy about using the Factorial Calculator to explore and verify your answers. It’s a great learning aid!

Frequently Asked Questions (FAQs)

Conclusion

Factorials are more than just a math symbol—they are a powerful tool that helps us count the endless possibilities in the world around us. From the simple arrangement of toys on a floor to the complex algorithms that power our technology, understanding factorials opens a door to a deeper appreciation of mathematics.

We hope this guide has made the concept clear and even a little fun! The next time you need to calculate a factorial, whether for a homework assignment or just to satisfy your curiosity, remember that our Factorial Calculator on Calculatorsera.com is just a click away. It’s fast, simple, and a fantastic way to explore the incredible, rapid growth of numbers. Give it a try today

Thank you for reading this post, don't forget to subscribe!